Aportes de euclides a la geometria: Propone un sistema de estudio en el que se da por sentado la veracidad de ciertas proposiciones por ser intuitivamente claras llamadas: axiomas o postulados y a partir de ellas se deducen todos los demas resultados.
lunes, 7 de febrero de 2011
INTRODUCCION A LA GEOMETRIA
Geometría: Es una rama de la matemática que se ocupa de las propiedades de las figuras geométricas en el plano o el espacio, como son: puntos, rectas, planos, polígonos, poliedros, paralelas, perpendiculares, curvas, superficies, etc. Sus orígenes se remontan a la solución de problemas concretos relativos a medidas y es la justificación teórica de muchos instrumentos, por ejemplo el compás, el teodolito y el pantógrafo. Tiene su aplicación práctica en física, mecánica, cartografía, astronomía, náutica, topografía, balística, etc. También da fundamento teórico a inventos como el sistema de posicionamiento global.
Principales precursores de la geometria: Copérnico (1473-1543) , Kepler (1571,1630), para las relaciones trigonométricas.
*Jordano Nemorarius (1237-?) a quien debemos la primera formulación correcta del problema del plano inclinado.
*Nicole Oresmes (1328-1382) llegó a utilizar en una de sus obras coordenadas rectangulares, aunque de forma rudimentaria, para la representación gráfica de ciertos fenómenos físicos.
*el matemático egipcio Abu Kamil enunció y demostró las leyes fundamentales e identidades del álgebra, y resolvió problemas tan complicados como encontrar las x, y, z que cumplen x + y + z = 10, x2 + y2 = z2, y xz = y2.
*Los matemáticos alejandrinos Herón y Diofante continuaron con la tradición de Egipto y Babilonia, aunque el libro Las aritméticas de Diofante es de bastante más nivel y presenta muchas soluciones sorprendentes para ecuaciones indeterminadas difíciles.
*Los matemáticos alejandrinos Herón y Diofante continuaron con la tradición de Egipto y Babilonia, aunque el libro Las aritméticas de Diofante es de bastante más nivel y presenta muchas soluciones sorprendentes para ecuaciones indeterminadas difíciles.
*Las puertas a la Geometría Analítica fueron abiertas, ya en el siglo XVII por Descartes y Fermat, pero sólo incluían problemas planos.
*Jordano Nemorarius (1237-?) a quien debemos la primera formulación correcta del problema del plano inclinado.
*Nicole Oresmes (1328-1382) llegó a utilizar en una de sus obras coordenadas rectangulares, aunque de forma rudimentaria, para la representación gráfica de ciertos fenómenos físicos.
*el matemático egipcio Abu Kamil enunció y demostró las leyes fundamentales e identidades del álgebra, y resolvió problemas tan complicados como encontrar las x, y, z que cumplen x + y + z = 10, x2 + y2 = z2, y xz = y2.
*Los matemáticos alejandrinos Herón y Diofante continuaron con la tradición de Egipto y Babilonia, aunque el libro Las aritméticas de Diofante es de bastante más nivel y presenta muchas soluciones sorprendentes para ecuaciones indeterminadas difíciles.
*Los matemáticos alejandrinos Herón y Diofante continuaron con la tradición de Egipto y Babilonia, aunque el libro Las aritméticas de Diofante es de bastante más nivel y presenta muchas soluciones sorprendentes para ecuaciones indeterminadas difíciles.
*Las puertas a la Geometría Analítica fueron abiertas, ya en el siglo XVII por Descartes y Fermat, pero sólo incluían problemas planos.
Aportes de pitagoras a la geometria: estudio los numeros clasificandolos segun sus propiedades bien definidas, descubrio los numeros amistosos, perfectos, abundantes, deficientes e inicio el estudio de los numeros figurados. Tambien se le debe la definicion del puntos como unidad de pisicion, la clasificacion de los angulos y la concepcion geometrica del espacio.
Punto: concepto basico geometrico no definido que carece de longitud, anchura y espesor, su idea puede sugerirse por la huella que deja un lapiz bien afilado en el papel
Linea: concepto geometrico no definido que posee longitud pero carece de anchura y espesor.
 .
.



Linea: concepto geometrico no definido que posee longitud pero carece de anchura y espesor.
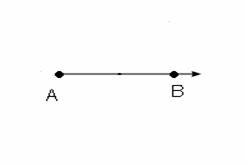
Puntos colineales: puntos que estan sobre una misma recta. en la siguiente figura se muestra que los puntos A y B son colineales
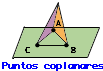
Puntos coplanares: puntos que se encuentran sobre un mismo plano como se muestra en la siguiente figura.
 .
.Angulo: es la figura geometrica formada por la union de dos segmentos (rayos) de origen comun. Las semirrectas se llaman lados y el punto de origen comun se denomina vertice.
Bisectriz: Semirrecta que tiene como origen el vertice de un angulo y lo divide en dos angulos de igual magnitud
Poligono: figura geometrica limitada por segmentos de recta que se denominan lados, el poligono de menor numero de lados se llama triangulo.
Circunferencia: es una curva cerrada en donde los puntos estan en un mismo plano, y son equidistantes de un punto fijo llamado centro. Cualquier segmento de recta que una al cento con parte de la circunferencia se llama radio.

Angulo central: es el angulo cuyo vertice esta en el centro de la circunferencia.
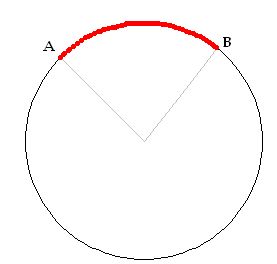
Arco: si se eligen dos puntos de una circunferencia,estos limitan dos porciones cada una de ellas llamadas arco.

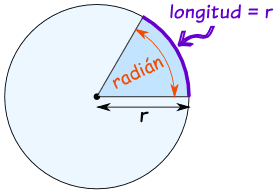
Radian: 2π(1 rad) = 360*
1 rad= 360*/ 2π
1 rad= 180*/ π = 57*17`45"
Suscribirse a:
Comentarios (Atom)